The Natural Numbers Game

A journey of a thousand miles begins with a single step. – Lao Tsu

Welcome to the Prooftoys edition of the Natural Numbers Game, a series of problem-solving challenges in which you build mathematical knowledge about numbers step by step with computer guidance. As you take on the challenges of the game you build skills in creating 100% correct mathematical proofs.

This sequence of pages is designed to be self-contained with enough information to give you a practical introduction to proving and problem-solving with Prooftoys. The Prooftoys documentation has more systematic and in-depth explanations.

What is this about?

You will start with just the bare essentials of knowledge about the natural numbers (the “counting numbers”, 0, 1, 2, 3, and so on up from there) and work your way up to more powerful knowledge through mathematical proofs.

The structure of this game is largely a clone of the Natural Number Game tutorial developed in England at Imperial College London using the Lean Theorem Prover. This edition uses the Prooftoys proof assistant, with its focus on graphical user interaction, simplicity, and ease of use for beginners. While it knows far less mathematics than research-grade proof assistants such as Lean, the logic of Prooftoys is capable of supporting advanced university-level math.

Will it be hard?

If you have studied basic high school algebra, you have encountered the concepts you will need! In fact it turns out that there are fundamentally only two ways for Prooftoys to deduce one true statement to another, and these are both part of ordinary high school algebra. You will probably recognize the principles when you see them in action, and Prooftoys will provide you with guidance and suggestions to help you succeed.

Your first mission, should you decide to accept it, is to prove that 0 = 0 — about as simple as it gets.

The tiny one-step proof of this will use the principle that anything is equal to itself. As trivial as it is, it shows a great deal about using Prooftoys.

What is this?

In front of you is a Prooftoys proof editor. It displays a proof in progress, and lets you interactively add to or modify the proof, experimenting with different proof steps and approaches.

You should see the beginning of a proof, with just one line. If not, click on “Clear work”, then confirm that you want to clear your work. The initial statement in this case is 0 = 0 => 0 = 0.

This will be a goal-directed proof. The proofs in this whole section are generally set up in this style, so we show this one in the goal-directed style to introduce you to the style even though being goal-directed does not really help you here. The first line of this proof says that if 0 = 0 then 0 = 0.

The idea of goal-directed proof in Prooftoys is that you work with a sequence of true statements, each with the desired conclusion, but having extra assumptions that are not in the goal statement. In your proof you eliminate undesired assumptions until only the stated goal remains.

Taking your first step

First steps are big milestones! This proof will have just one step. To do this proof step you will select a part of the initial step, then choose one of the suggested actions in the menu.

Start by selecting the assumption, the first 0 = 0. For an ultra-quick demo click here. As you hover the mouse over different parts of the step, they highlight, and when you click there is a stronger highlight that stays until you click again.

After selecting the first 0 = 0, move the mouse down into the “Basic” section of the menu, and select the menu item that says ➭ T using x = x == T by clicking on it. another tiny demo The ➭ T in the menu item means that it will replace the selected term with T. In proofs we like to replace assumptions with T because that removes the assumption from the list, which usually brings us closer to the goal.

If the “Basic” section of the menu is not already displayed, show it by pausing the mouse cursor over the word “Basic”.

The arrow at the beginning of the menu item means that the term you have selected will be replaced with T, for true. Many typical proof steps are like this, replacing an assumption.

Now that you have selected that menu item, you should see a second step in the proof editor display, and the words “Proof complete” at the top of the proof editor area, like in this picture. Congratulations, you did it!

This one proof step illustrates both of the basic operations Prooftoys uses to get from one true statement to another true statement: substitution as already described, and replacement of a term with some equal term. In this step, Prooftoys uses the fact that (x = x) == T to replace 0 = 0 with T, and when an assumption becomes T, it drops it from the assumptions.

Operator ==: The == operator tests for equality just like the usual =, but is specifically for true/false values unlike =, which is generic.

(It might seem as if “dropping” assumptions is based on some additional, special principle; but really behind the scenes it uses the same principles as all other reasoning, and Prooftoys can show you those details on request.)

The pieces

Operator =>: The statement (0 = 0) => (0 = 0) is a conditional statement because of the double arrow (=>) in the middle, which is the conditional operator. You can read a conditional statement A => B as A implies B, or if A then B. Items on the left side of a conditional are considered assumptions. The meaning of a conditional statement is, “if all of the assumptions are true, then the conclusion is true.” This statement has only one assumption: 0 = 0.

The part of the statement after the conditional operator is the conclusion; in this case the 0 = 0 on the right. All of these parts, and any meaningful part of a a mathematical statement, such as the assumptions and the conclusion we call a term.

We say that this statement has the form A => A because it has the same statement on the left and on the right of the => operator. If you replace both of the A’s with 0 = 0 you get 0 = 0 => 0 = 0. Replacement of all occurrences of a variable with the same term is substitution – one of the two fundamental ways of getting from one true statement to another in the logic of Prooftoys.

This combination of substitution followed by replacement is known as rewriting, our most widely used type of proof step. So it is fair to say that this simple one step proof sets the stage for all reasoning in Prooftoys.

➪ Next

About the Proof Editor

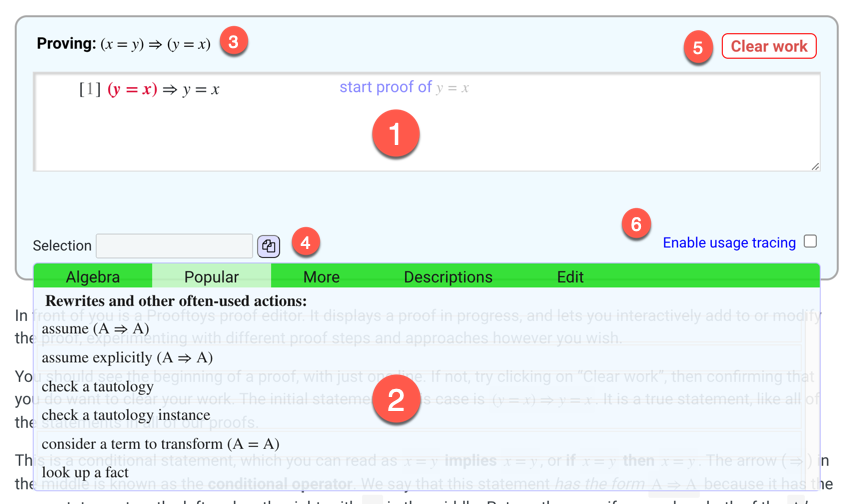
Here is a quick visual reference to the parts of a proof editor. The labeled parts are:

1. Proof display. This shows the steps of your proof so far. It lets you select steps or parts of steps, or delete steps easily.
2. Action menu. This menu is dynamic based on the current selection in the proof display. Selecting items here is the way you develop and edit proofs.
3. Goal statement. This shows what you are trying to prove. If it has the form A => B, A has the expected assumptions for proving the conclusion B.
4. Copy text. This lets you copy the most recently-selected term as text.
5. Clear work. Use this button to restart the proof from the beginning.
6. Checking this box gives the developer permission to generate detailed traces of your activity for research purposes, to improve the website and the proof editor. See the privacy information page for details.

➪ Next