Using the Proof Builder

Contents

This page and the Youtube video explain use of the proof builder user interface. Go to the principles of reasoning page for more understanding.

The worksheet

The first time you visit a page that contains a proof builder, the proof builder looks a bit like a window onto a blank sheet of paper with a few controls. This proof display will show the steps of your proof in progress with a brief description of each step, but for now it is blank. You will fill it in with deduction steps by selecting steps or parts of steps, choosing items from menus, and entering terms (expressions) in the language of the Prooftoys logic.

Each time your worksheet changes, it is stored persistently in your web browser, so you can navigate to other pages and return, or even power off your computer, and still keep your work as long as you like. Just remember that worksheets are not shared across different web browsers, even on the same computer.

You can have many worksheets, and switch back and forth between them with the proof builder, using the “Worksheets” button and its menus. The name of the current worksheet is displayed at the top of the proof builder display. You can also browse a list of all of your worksheets. Clicking on the “Worksheets” button shows you additional controls. Then choose “Open” to see the list of worksheets.

Starting a proof

When you hover the mouse over the worksheet an additional area with menus will appear at the bottom:

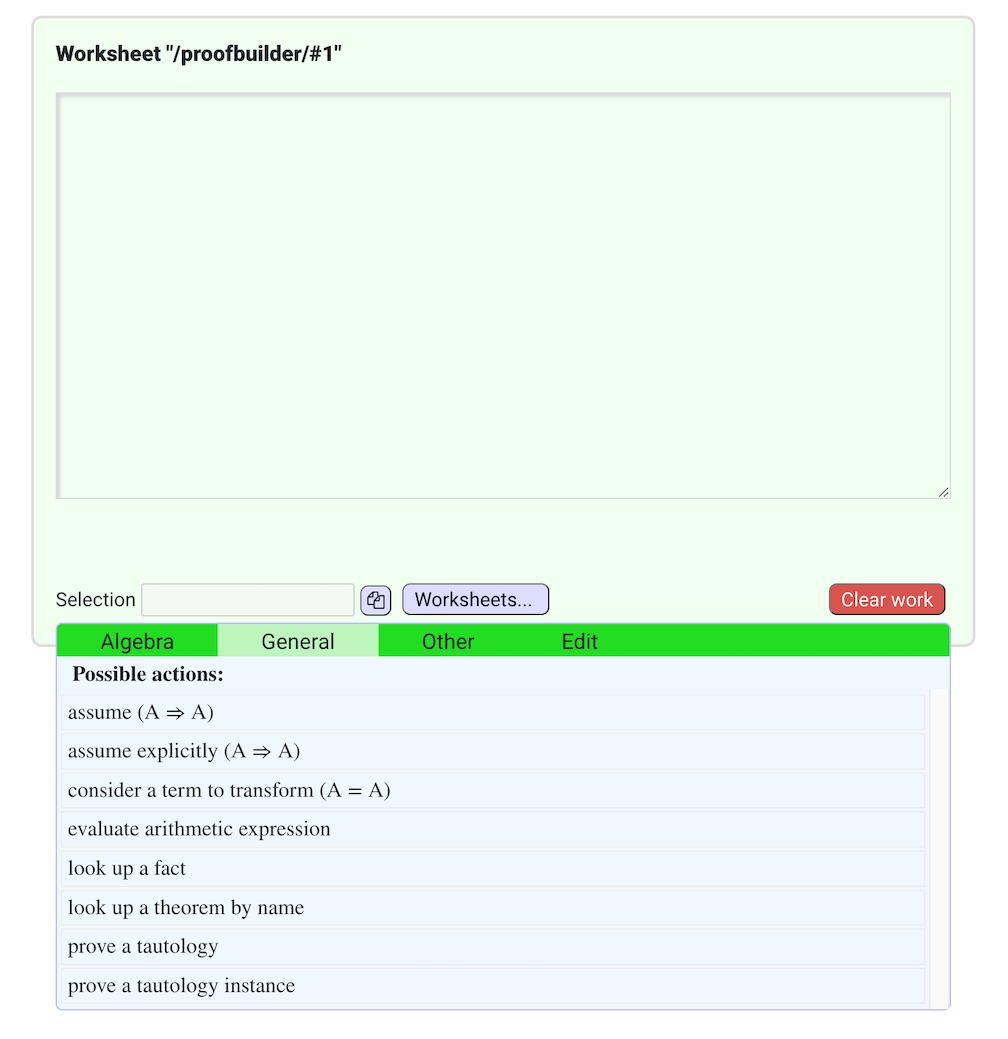
The “General” menu is initially active with its heading highlighted, but you can activate any menu by hovering over its heading. The menus are sensitive to your selection of a step or term (expression) within a step, but since there are no steps to select, the menu shows only actions that create a new step, not depending on any existing proof step.

Selecting any one of these prompts you to enter an expression in the language of the logic. All of these prove the step they generate, so do not hesitate to use them whenever they may be useful.

assume and assume explicitly

These create an “assumption” step, an example of the fact that any statement implies itself. The only difference is in the display. Enter any term with a boolean value to assume it.

consider a term to transform

This creates an example of the fact that any term is equal / equivalent to itself. Enter a valid term, which the proof builder will prove equal to itself. The display of this step only shows the right-hand side of the equation.

look up a fact

Prooftoys knows basic logic and facts about real numbers. When you select a term, Prooftoys searches automatically for relevant facts to apply based on the currently selected step or term, so you can often choose and apply a fact from the menus without having to type it in.

You can also enter a fact known to Prooftoys using the keyboard. If the conclusion of a conditional fact uniquely identifies it, you can omit the assumptions. You can also enter an arbitrary tautology this way, and Prooftoys will prove it for you.

Prooftoys can also prove an arbitrary tautology or a substitution instance of a tautology through this menu item.

prove a tautology

This attempts to prove the input statement as a tautology. It currently supports boolean functions “and”, “or”, “not”, boolean equality (either “=” or “==” each with its own precedence), and the conditional ("=>").

prove a tautology instance

This checks whether the formula you enter is the result of a substitution into a tautology. If so it proves the tautology and does the substitution for you.

Try it. Select “assume explicitly (A => A)” in the menu. Prooftoys will prompt you for a term to assume. Enter \P == x * x = x and press the Return key or click on the Go button next to the input field. This invites you to find a solution term equivalent to x * x = x. (Open the proof builder page.)

Inference steps

Most steps in proofs build from one step to another step. In the proof builder, creation of a new proof step is usually done by first selecting a step or part of a step, then selecting an item from one of the menus.

Selecting a step or term

To select a step, click on its step number, or on the checkbox adjacent to the step number. You will see the step highlight, and the highlight will remain until you click somewhere else, either clearing it or selecting something different.

If you hover the mouse over different parts of a step, the different terms in the step will highlight as you hover. If you click while a term is highlighted, the highlight appearance will change, and will remain as you move the mouse elsewhere. As with a step, a term remains selected until you click somewhere else, either clearing it or selecting something different. You can only select one thing at a time in Prooftoys.

The content of the menus is sensitive to the selection. When you select a step or term you will usually see the visible menu change accordingly.

Try it. Select the last x in x * x = x, the one on the right side of the equation. (Open the proof builder page.)

Using the menus

Some rules such as “assume” take input from you, as we saw above. When you hover the mouse over one of these menu items, the preview area shows a message like “needs user input”. Other rules only need the current selection to do their work.

The proof builder also searches through its library of registered facts and through the steps in your proof so far for ones it can use with its basic types of inferences. It shows information about the action in the menu, and if you hover over the item, it shows exactly what the result would be.

Even if a menu item is offered, it is not always guaranteed that the action can be accomplished. When you hover over the item, the proof builder will try to actually perform the action. If the action cannot be done, the preview will be a message such as “nothing to do”. In that case, choosing the menu item has no effect.

Try it. In our example we will subtract x from both sides of the equation, which is an algebra step. This will allow it to be removed from the right side of the equation. Use the “algebra” menu, and hover over the menu item labeled “subtract ☆ from both sides”. The proof builder will preview the result of the step at the bottom of the worksheet display. Now choose the menu item with a click. (Open the proof builder page.)

Prooftoys will show you the result of this step and automatically add a “simplify” step that cancels out the resulting x - x term on the right hand side.

The proof builder always adds new steps at the end of the proof.

The menus

Algebra. Many of the items in the algebra menu, like “subtract from both sides” in the example, do proof procedures that are useful in manipulating equations, as in basic textbook math. The algebra menu also presents a few facts about real numbers that are often useful in basic algebra.

General. When a step or term in the proof is selected, the general menu offers to apply commonly useful facts that can operate on that step or term in the ways Prooftoys uses facts in proofs.

Other. More matches of the selection with steps in your proof and standard inferences that can use them. These are estimated to be less often useful or more advanced than ones in the general menu.

Edit. If a step has no other steps that depend on it, you can delete it with the red circled “x” next to it. The “Edit” manu offers additional proof editing commands.

Hints and tips

Tips for entering facts

Certain kinds of commonly-occurring assumptions can be omitted when you enter a fact using the keyboard. In particular you can omit assumptions that variables must be real numbers, such as R x (“x is a real number”) and conditions that a variable cannot be zero, as in x / x = 1. In many simple cases this means you do not need to enter any assumptions at all.

For example the commutative law for real numbers can be entered as simply x + y = y + x.

It doesn’t matter which names you use when entering a fact. Entering the fact as w + z = z + w would have the same effect.

About matching

Practical reasoning in Prooftoys is built primarily on rewriting and forward reasoning.

These both match a selected term in a proof step with part of some other registered fact or step in your proof. This is the same kind of matching taught in any basic algebra textbook. There is more detailed information in the section on principles of reasoning in Prooftoys at rewriting and forward reasoning.

Reading and understanding proof displays

The main content of a proof editor is a proof display that shows the steps of the proof being built. There are also plain proof displays that are not editable, and they provide most of the same information as proof displays in a proof editor.

Each of the steps in a proof editor has a step number that identifies it. These numbers are sequential, starting at number 1. The display of the step shows its statement, possibly omitting the step’s assumptions if they are the same as in the preceding step. If the assumptions are omitted you will see an ellipsis (like “…"). You can see the entire step with all assumptions by hovering over the ellipsis.

After the display of the step’s statement is a brief description of the inference that justifies the step.

If you hover the mouse over different parts of a proof step you will see parts of the step lightly outlined. All of these areas are subexpressions of the proof step, also known as its terms. If the display is editable you can select any of these by clicking on it.

If you hover the mouse over a step’s step number, the proof display will show information about the steps and/or terms that this step depends on. This information varies, but in general it highlights a full step by highlighting its step number, or a term within the step by highlighting the term. If it highlights a term, that is usually the term that was selected to do the inference step, such as the term modified by a rewrite rule.

Hovering over the step number will also gently highlight references to the step from displays of other steps.

Part of the description of each step is presented in blue. Clicking on this word or phrase causes the display to show you a level of detail in the proof. You can potentially reach this until reaching axioms of the mathematical system and fundamental inference steps of the logic.

Managing worksheets

TBD